Recherche dichotomique

⏬

1 - Trier

2 - Principe

3 - Algorithme

4 - Python

5 - FAQ

Nous avons vu que parcourir un tableau élément par élément nécessite un algorithme dont le coût est linéaire : sa complexité est Θ(n).

Nous allons voir aujourd'hui comment faire mieux que cela mais sur un tableau particulier : un tableau trié.

Logiciel nécessaire pour l'activité : Python 3 : Spyder, Pyzo, IDLE ou le site repl.it ...

A RENDRE ✎ : Partie 2 Principe de la recherche:L'exercice 5 et Partie 4 Python Exercice (question 2 a et b)

1 - Trier un tableau avec Python

⇩ ⇧ ⤊

Rappel

L'opération de tri est fondamentale en informatique.

En réalité, lorsqu'on sait qu'on va régulièrement devoir rajouter des données dans un tableau, on doit se demander si on les rajoute simplement à la fin du fichier ou si on s's'arrange plutôt pour insérer le nouvel enregistrement entre les deux bons enregistrements de façon à avoir une collection triée par rapport au descripteur/attribut le plus courant.

Nous allons voir comment faire dans le cas des tables plus tard : aujourd'hui, on va se limiter à de simples tableaux. C'est déjà bien assez compliqué.

a. Génération aléatoire d'un tableau

Commençons par créer un programme qui va nous générer un tableau aléatoire d'entiers compris entre 0 et 100.

Les deux fonctions renvoient exactement la même chose mais créent à l'interne le tableau de deux façons différentes :

La fonction creer crée un tableau renvoyé par compréhension.
La fonction creer2 crée un tableau renvoyé par extension (avec la méthode append).

Pour l'utilisateur, c'est totalement transparent : la fonction semble faire la même chose.

import random
 
def creer(nbr) :
    '''Fonction qui renvoie un tableau  de nbr éléments compris entre 0 et 100
 
    :: param nbr(int) :: un entier correspondant au nombre d'éléments voulus
    :: return (list) :: un tableau d'entiers de nbr éléments compris entre 0 et 100
    '''
 
    tableau = [random.randint(0,100) for x in range(nbr)]
    return tableau
 
def creer2(nbr) :
    '''Fonction qui renvoie un tableau  de nbr éléments compris entre 0 et 100
 
    :: param nbr(int) :: un entier correspondant au nombre d'éléments voulus
    :: return (list) :: un tableau d'entiers de nbr éléments compris entre 0 et 100
    '''
 
    tableau = []
    for index in range(nbr) :
        tableau.append(random.randint(0,100))
    return tableau


>>> creer(5)
[81, 78, 52, 42, 25]
>>> creer2(5)
[73, 62, 88, 69, 81]

01° Tester les deux fonctions dans le l'interpréteur Python. Par exemple en créant des listes de 10 ou 50 éléments.

En tapant help(creer) dans le Shell, dire si le créateur de la fonction a clairement préciser la précondition sur l'argument : à savoir qu'on doit envoyer un entier ?

Correction ?

...CORRECTION...


>>> help(creer)
Help on function creer in module __main__:
 
creer(nbr)
    Fonction qui renvoie un tableau  de nbr éléments compris entre 0 et 100

    :: param nbr(int) :: un entier correspondant au nombre d'éléments voulus
    :: return (list) :: un tableau d'entiers de nbr éléments compris entre 0 et 100

Donc, oui, c'est clairement noté qu'on doit fournir un entier.

Il n'empêche que rien n'oblige l'utilisateur à envoyer un entier. Il peut très bien le faire. Mais ça provoque une erreur. Et c'est de sa faute, vous lui aviez dit !

Si on veut stocker le résultat fourni par la fonction, il faudra le stocker dans une variable.


>>> tab1 = creer(5)
>>> tab2 = creer2(10)
>>> tab1
[11, 34, 31, 56, 88]
>>> tab2
[13, 55, 54, 57, 12, 80, 16, 72, 30, 99]

b. Coût d'un algorithme de recherche linéaire

Nous avions vu que le coût d'une recherche linéaire est en n puisqu'il faut lire les éléments un par un jusqu'à trouver l'élément ou arriver au bout du tableau.

Dans le pire des cas (l'élément cherché n'est pas dans le tableau), on va donc avoir à lire tous les index un par un.

Nous avions écrit que cet algorithme est en Θ(n).

Exemple : cherchons 2 dans [13, 55, 54, 57, 12, 80, 16, 72, 30, 99].

Nous allons devoir lire les 10 éléments : d'abord 13, puis 55, puis 54 ...

Si le tableau contenait 1000 éléments, il aura fallu lire 1000 éléments.

D'où la notion de coût linéaire ou Θ(n) : si le tableau comporte n éléments, l'algorithme aura à faire en gros n étapes dans le pire des cas.

c. Trier un tableau

Oui mais... on peut faire mieux. On peut travailler sur un tableau trié. Ce sera plus simple non ?

L'une des activités sur les algorithmes va être de réaliser ce tri. Mais comme c'est une opération très importante en informatique, tous les langages possèdent une ou des fonctions qui permettent de faire cela de façon efficace.

Nous allons en voir deux avec Python.

1 - Fonction native sorted

La fonction native sorted renvoie un tableau équivalent au premier mais trié.

Cela veut dire que le tableau originel n'est pas modifié : il est toujours dans le désordre.


>>> tab_initial = creer2(10)
>>> tab_initial
[13, 55, 54, 57, 12, 80, 16, 72, 30, 99]
 
>>> tab_trie = sorted(tab2)
>>> tab_trie
[12, 13, 16, 30, 54, 55, 57, 72, 80, 99]
 
>>> tab_initial
[13, 55, 54, 57, 12, 80, 16, 72, 30, 99]

Avantage : on garde en mémoire la configuration initiale des donnnées
Désavantage : ça prend deux fois plus de place mémoire. Avec 96 milliards de données de 4 octets, ça peut être important...

2 - Méthode sort

La méthode sort modifie sur place le tableau sur lequel on fait agir cette méthode.


>>> tab_initial = creer2(10)
>>> tab_initial
[13, 55, 54, 57, 12, 80, 16, 72, 30, 99]
 
>>> tab_initial.sort()
>>> tab_initial
[12, 13, 16, 30, 54, 55, 57, 72, 80, 99]

Avantage : moins de place mémoire nécessaire
Désavantage : si on veut retrouver l'état initial, il faut espérer que les données initiales sont stockées ailleurs que dans ce tableau.

✎ 02° Utiliser une instruction dans l'interpéteur (une des deux façons de faire précédentes) pour obtenir une version triée du tableau ci-dessous.
Fournir les instructions et le tableau trié.


tableau = [49, 13, 95, 90, 57, 82, 13, 59, 1, 11, 55, 25, 23, 66, 60, 76, 88, 10, 86, 60, 57, 35, 3, 62, 65, 22, 95, 33, 5, 76, 93, 24, 98, 16, 20, 70, 68, 47, 61, 19, 60, 6, 16, 37, 36, 96, 80, 28, 0, 54, 99, 65, 90, 71, 88, 41, 86, 81, 42, 38, 15, 62, 79, 46, 63, 100, 68, 45, 99, 41, 30, 91, 15, 77, 2, 83, 11, 52, 52, 7, 40, 29, 32, 32, 32, 17, 34, 42, 71, 73, 94, 75, 69, 30, 85, 98, 42, 34, 86, 54]

Le plus beau, c'est que ça fonctionne aussi avec les strings.
On peut ainsi trier une liste de mots par ordre alphabétique.

2 - Principe de la recherche dichotomique

⇩ ⇧ ⤊

Si les tableaux s'affichent sans couleur ou si les animations semblent ne pas fonctionner, il faut que vous relanciez la page à jour de façon à mettre vos fichiers CSS à jour.

La condition de base pour pouvoir réaliser cette recherche est d'avoir un tableau trié.

Par exemple avec un tableau trié de 20 éléments et donc d'index compris entre 1 et 20.

6, 8, 9, 13, 18, 37, 37, 59, 60, 60, 61, 68, 70, 80, 80, 83, 83, 89, 91, 96

Sous forme d'un tableau, ce sera plus facile.

	↦																			↤
Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

a. Cherchons si 40 est présent dans ce tableau.

En recherche séquentielle, on regarderait l'index 1 (6), l'index 2 (8)... Ici, il faut donc 20 boucles et 20 comparaisons.

En recherche dichotomique, nous allons systématiquement supprimer la moitié des données restantes en comparant la valeur associée à l'index central. Si la valeur n'est pas la bonne, on ne gardera que la partie restante à droite ou à gauche.

Etape 1 - Intervalle de départ [1 ; 20]

on considère un point gauche d'index 1 : gauche = 1.
on considère un point droite d'index 20 : droite = 20.
On calcule l'index central ou milieu à l'aide d'un division entière : (1+20)//2 donne 10 On aura donc milieu = 10.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme tableau[10] = 60 et qu'on cherche 40 dans un tableau trié, on ne garde que la partie à gauche du point central d'index 10.

On va alors changer le point droit avec droite = 9

On recommence ces opérations sur le nouvel intervalle [1 ; 9].

Etape 2 : Intervalle [1 ; 9]

on considère un point gauche d'index 1 : gauche = 1.
on considère un point droite d'index 9 : droite = 9.
On calcule l'index central ou milieu à l'aide d'un division entière : (1+9)//2 donne 5 On aura donc milieu = 5.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 5 fait référence à 18 et qu'on cherche 40 dans un tableau trié, on ne garde que la partie à droite de l'index 5.

On va alors changer le point gauche avec gauche = 6

On recommence ces opérations sur le nouvel intervalle [6 ; 9].

Etape 3 : Intervalle [6 ; 9]

on considère un point gauche d'index 6 : gauche = 6.
on considère un point droite d'index 9 : droite = 9.
On calcule l'index central ou milieu à l'aide d'un division entière : (6+9)//2 donne 7 On aura donc milieu = 7.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 7 fait référence à 37 et qu'on cherche 40 dans un tableau trié, on ne garde que la partie à droite de l'index 7.

On va alors changer le point gauche avec gauche = 8

On recommence ces opérations sur l'intervalle [8 ; 9].

Etape 4 : Intervalle [8 ; 9]

on considère un point gauche d'index 8 : gauche = 8.
on considère un point droite d'index 9 : droite = 9.
On calcule l'index central ou milieu à l'aide d'un division entière : (8+9)//2 donne 8 On aura donc milieu = 8.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 8 fait référence à 59 et qu'on cherche 40 dans un tableau trié, on ne garde que la partie à gauche de l'index 8.

Du coup, on obtient un ensemble vide.

Pas d'étape 5 : l'intervalle restant est vide : l'index droit vaut 7, moins que l'index gauche qui vaut 8 !

Conclusion : 40 n'appartient pas à notre tableau.

Réponse obtenue avec 4 comparaisons. C'est mieux que 20 non ?

Pour résumer

Si vous voulez revoir la progression de la recherche, voici l'animation globale.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

On peut aussi possible de représenter le principe de l'algorithme de recherche dichotomique avec le schéma suivant:

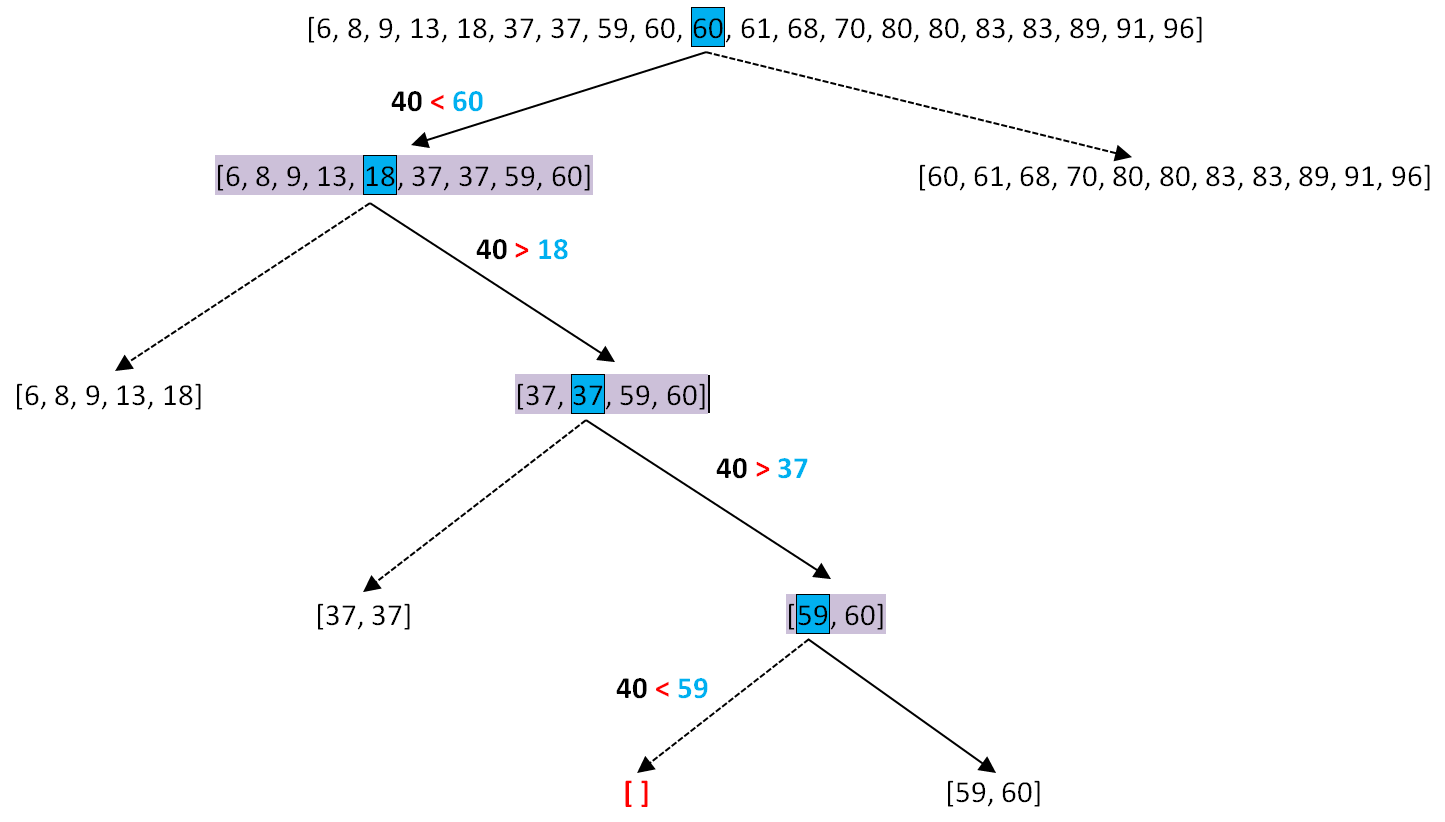
La liste finale est vide , donc 40 n'est pas dans la liste.

b. Cherchons si 70 est présent dans ce tableau.

En recherche séquentielle, on regarderait l'index 1 (6) à l'index 13 (70)... Ici, il faut donc 13 boucles et 13 comparaisons.

Recherche dichotomique pour 70

c. Exercice

03°

Réaliser une recherche dichotomique de 50 dans le tableau ci-dessous.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Elément	18	23	25	35	48	50	58	68	70	73	75	79	80	82	85	89

L'intervalle initiale de l'étape 1 est donc [1 ; 16].

Gauche est placé à 1 et droite est placé à 16.

Le travail se fait à la main. Répondre aux questions ci-dessous et ensuite faire un schéma récapitulatif.

Questions

Que vaut l'index central de l'étape 1 ?
Que vaut l'intervalle au début de l'étape 2 ?
Que vaut l'index central de l'étape 2 ?
Que vaut l'intervalle au début de l'étape 3 ?
Que vaut l'index central de l'étape 3 ?

✎ 04°

Combien de comparaisons ont été faites pour effectuer cette recherche.
Combien de comparaisons aurait-on dû faire avec une recherche séquentielle ?

✎ 05°

a) Représentez le principe de fonctionnement de l'algorithme (pour le cas T = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 9) à l'aide d'un schéma

b) Représentez le principe de fonctionnement de l'algorithme (pour le cas t = [5, 7, 12, 14, 23, 27, 35, 40, 41, 45] et x = 40) à l'aide d'un schéma

Nombre d'étapes maximales

Puisqu'on divise à chaque fois l'intervalle restant par deux, on peut prévoir le nombre maximale d'étapes dans le pire des cas lorsqu'on effectue une recherche par dichotomie.

Exemple avec un tableau de 16 valeurs (16 pouvant s'écrire 2⁴ ):

Etape 1 : une comparaison sur un ensemble de 16 valeurs : 8 d'un côté, le pilier et 7 de l'autre.
Etape 2 : une comparaison sur au pire 8 valeurs : 4 d'un coté, le pilier et 3 de l'autre .
Etape 3 : une comparaison sur au pire 4 valeurs : 2 d'un côté, le pilier et 1 de l'autre.
Etape 4 : une comparaison sur au pire 2 valeurs : le pilier et l'autre valeur.
Etape finale avec la comparaison sur la dernière valeur possible.

Exemple avec un tableau de 32 valeurs (32 pouvant s'écrire 2⁵ ):

Etape 1 : une comparaison sur un ensemble de 32 valeurs.
Etape 2 : une comparaison sur au pire 16 valeurs.
Etape 3 : une comparaison sur au pire 8 valeurs.
Etape 4 : une comparaison sur au pire 4 valeurs.
Etape 5 : une comparaison sur au pire 2 valeurs.
Etape finale avec la comparaison sur la dernière valeur possible.

On voit donc que si un nombre n est dans l'intervalle ] 2^X-1 ; 2^X ], on aura besoin au pire de X+1 comparaisons pour trouver ou non si un élément appartient à ce tableau.

On parle d'un coût logarithmique et on peut écrire que cet algorithme est sur le pire des cas Θ(log₂ n).
On va le montrer un peu plus tard

C'est bien entendu bien mieux que dans le cas de la recherche séquentielle.

A titre d'exemple, sur un tableau d'un million de valeurs,

On a besoin de 1 000 000 de comparaisons dans le pire des cas avec une recherche séquentielle
On a besoin de 20 comparaisons avec une recherche dichotomique !

Ceux qui le désirent pourront voir en fin d'activité pourquoi on peut écrire cela mathématiquement, mais c'est hors programme pour la 1er NSI. Mais c'est intéressant pour ceux qui s'intéressent à l'informatique et ça vous donnera une première approche du logarithme.

Par contre, n'oubliez pas que le tableau doit être trié.

Si vous voulez vous amuser à prévoir le nombre de coups sur différents exemples, voici un tableau automatisée où vous pouvez créer des valeurs aléatoires et faire une recherche sur une valeur donnée.

Valeur cherchée :


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

3 - Algorithme et Preuve de terminaison

⇩ ⇧ ⤊

a. Algorithme

Commençons par présenter l'algorithme maintenant que vous parvenez à l'appliquer.

Algorithme de recherche dichotomique

But : trouver si un élément recherché existe bien dans un tableau. S'il existe, il renvoie le booleen VRAI (True). Sinon, il renvoie FAUX(False).

Principe : dans un tableau trié, on regarde la valeur centrale dans les index encore disponibles. S'il ne s'agit pas de la bonne valeur, on enlève de l'intervalle de recherche les index qui ne peuvent pas contenir la valeur recherchée.

Description des entrées / sortie

ENTREES :

tableau : un tableau trié contenant un ensemble d'éléments.
x : un élément voulu qu'on tente de rechercher dans le tableau
(optionnelle selon les langages d'implantation): longueur, le nombre d'éléments dans le tableau

SORTIE : un booleen.

Algorithme commenté

Dans l'algorithme ci-dessous, l'opérateur // désigne un commentaire.

gauche ← 1

droite ← longueur

TANT QUE gauche <= droite

milieu ← Ent((gauche + droite) / 2)

// partie entière

SI tableau[milieu] = x

// On a trouvé la valeur x dans le tableau à la position milieu

Renvoyer Vrai

SINON SI tableau[milieu] > x

// on ne garde que ce qui est à gauche du milieu. On cherche entre gauche et milieu - 1

droite ← milieu - 1

SINON

// on ne garde que ce qui est à droite du milieu. On cherche entre milieu + 1 et droite

gauche ← milieu + 1

Fin du Si

Fin Tant que

// Si on arrive ici, c'est que l'intervalle de recherche est vide. On est sorti de la boucle sans trouver x

Renvoyer Faux

Algorithme non commenté

gauche ← 1

d ← longueur

TANT QUE gauche <= droite

milieu ← Ent((gauche + droite) / 2)

SI tableau[milieu] = x

Renvoyer Vrai

SINON SI tableau[milieu] > x

droite ← milieu - 1

SINON

gauche ← milieu + 1

Fin du Si

Fin Tant que

Renvoyer Faux

Cet algorithme est la traduction directe des actions effectuées dans la partie précédente.

b. Terminaison

Cette notion sera abordé dans un autre chapitre

c. Complexité

Pour étudier la complexité, nous allons nous intéresser à la boucle : au niveau de la boucle, combien doit-on effectuer d'itérations pour un tableau de taille n
dans le cas le plus défavorable (l'entier x n'est pas dans le tableau t) ?

Sachant qu'à chaque itération de la boucle on divise le tableau en 2, cela revient donc à se demander combien de fois faut-il diviser le tableau en 2 pour obtenir, à la fin, un tableau comportant un seul entier ?
Autrement dit, combien de fois faut-il diviser n par 2 pour obtenir 1 ?

Mathématiquement cela se traduit par l'équation $\frac{n}{2^a}=1$ avec a le nombre de fois qu'il faut diviser n par 2 pour obtenir 1.
Il faut donc trouver a !

A ce stade il est nécessaire d'introduire une nouvelle notion mathématique : le "logarithme base 2" noté $log_2$ .
Par définition $log_2(2^x)=x$

Nous avons donc :

$\frac{n}{2^a}=1$ => $n=2^a$ => $log_2(n)=log_2(2^a)=a$ , nous avons donc $a=log_2(n)$

Nous pouvons donc dire que la complexité en temps dans le pire des cas de l'algorithme de recherche dichotomique est $O(log_2(n))$

Afin de pouvoir comparer l'efficacité des différents algorithmes, voici une représentation graphique des fonctions $y=x$ (en rouge), $y=x^2$ (en bleu) et $y=log_2(x)$ (en vert)

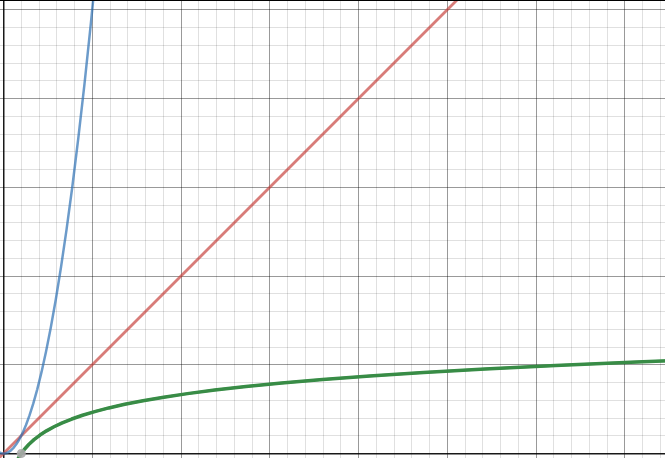
Comme vous pouvez le constater l'algorithme de recherche dichotomique est plus efficace que l'algorithme de recherche qui consiste à parcourir l'ensemble du tableau.
En effet $x>log_2(x)$ quelque soit $x$ .
Cependant, il ne faut pas perdre de vu que dans le cas de la recherche dichotomique, il est nécessaire d'avoir un tableau trié.
Si au départ le tableau n'est pas trié, il faut rajouter la durée du tri.

Nous étudirons quelque algorithme de tris un peu plus tard.

4 - Python

⇩ ⇧ ⤊

Exercice

Etant données un tableau T (i.e., une liste en Python) de n entiers triés par ordre croissant et un entier x

1. Ecrire une fonction Python qui recherche si l'entier x est dans le tableau T. Cette fonction renvoie un booléen 'vrai' si x est dans le tableau, sinon 'faux'.
Utliser la méthode de recherche par dichotomie (Cela revient à transcrire en python l'alorithme que l'on vient d'étudier)

2. On veut déterminer l'indice de l'entier x dans le tableau T. Si x n'apparaît pas dans T, on renvoie l'indice -1.

a) Une première solution pour ce problème est de parcourir le tableau dans l'ordre croissant jusqu'à trouver l'entier x ou jusqu'à le dépasser sans l'avoir trouvé.
Ecrire un programme en Python de cette première solution.

b) Une autre solution est de procéder par une recherche dichotomique.
Ecrire un programme en Python de cette deuxième solution.

5 - FAQ

⇩ ⇧ ⤊

J'ai également vu O(log₂ n). C'est quoi ce truc ?

Il s'agit de la fonction logarithme (ici en base 2).

C'est une fonction extrêmement utile : on peut la voir en première approximation comme la fonction qui renvoie la puissance de 2 permettant d'écrire le nombre.

Quelques exemples avec Python


>>> import math
>>> math.log2(1)
0.0

Pourquoi ? Simplement car 1 = 2⁰. On renvoie 0.


>>> math.log2(2)
1.0

Pourquoi ? Simplement car 2 = 2¹. On renvoie 1.


>>> math.log2(4)
2.0

Pourquoi ? Simplement car 4 = 2². On renvoie 2.


>>> math.log2(8)
3.0

Pourquoi ? Simplement car 8 = 2³. On renvoie 3.

Le mieux, c'est que cela fonctionne également avec les valeurs qui ne sont pas une puissance entière de 2 !


>>> math.log2(6)
2.584962500721156

Pourquoi ? Simplement car 6 = 2^{2.584962500721156}. On renvoie 2.584962500721156. Si vous avez bien compris l'activité sur les floats, vous devriez comprendre qu'il s'agit certainement d'une valeur approximative.

Il existe un logarithme pour toutes les bases possibles et imaginables.

Le logarithme base 10 donne ainsi log10(1000) = 3 puisque 1000 = 10³

Ou encore le logarithme népérien ln qui est en lien avec la fonction exponentielle : ln(20) = 2.995732273553991 car on peut écrire

20 = e^{2.995732273553991} ou encore
20 = exp(2.995732273553991)

Et c'est lié au fait qu'avec un tableau de 1 million d'éléments, la méthode dichotomique ne prend qu'une vingtaine d'étapes au pire

Oui.


>>> math.log2(1E6)
19.931568569324174

Log et Lg, c'est différent ?

Oui.

Lorsqu'on parle simplement de log, on parle du log dans une base donnée. Si c'est rien n'est précisé, c'est certainement la base 10.

Habituellement, si on note juste log, on parle du log10.

Si on note lg(x), on parle de log₂(x) dans un contexte informatique. Cela évite de noter log₁₀(x). On note juste lg(x)

Attention donc au contexte dans lequel apparaît un logarithme.

Log et Ln, c'est différent ?

Oui.

Lorsqu'on parle simplement de log, on parle du log dans une base donnée. Si c'est rien n'est précisé, c'est certainement la base 10.

Lorsqu'on parle de ln, on parle du logarithme népérien en mathématiques. Vous le verrez en terminale.

Sauf que dans les documents informatiques, on parle souvent du logarithmique base 2. On devrait le noter log2 ou log₂. Mais souvent, la complexité ou le coût apparaît sous la forme lg (voir au dessous) mais aussi parfois ln. Pourquoi ? Tout simplement car log₂(x) = ln (x) / ln (2). ln 2 n'est donc qu'un coefficient multiplicateur. C'est un peu comme un coût en 0.5n³ qu'on noterait juste n³.

Attention donc au contexte dans lequel apparaît un logarithme.

Petit résumé des notations

On voit juste log : c'est certainement log₁₀.

On voit juste lg : c'est certainement log₂.

On voit juste ln : c'est le logarithme népérien.

Activité publiée le 27 04 2020
Dernière modification : 27 04 2020
Auteurs : ows. h. et modifié par Pascal.F.

⏫

Recherche dichotomique

1 - Trier un tableau avec Python

Rappel

a. Génération aléatoire d'un tableau

b. Coût d'un algorithme de recherche linéaire

c. Trier un tableau

1 - Fonction native sorted

2 - Méthode sort

2 - Principe de la recherche dichotomique

Nombre d'étapes maximales

3 - Algorithme et Preuve de terminaison

a. Algorithme

Algorithme de recherche dichotomique

b. Terminaison

c. Complexité

4 - Python

5 - FAQ

J'ai également vu O(log2 n). C'est quoi ce truc ?

Et c'est lié au fait qu'avec un tableau de 1 million d'éléments, la méthode dichotomique ne prend qu'une vingtaine d'étapes au pire

Log et Lg, c'est différent ?

Log et Ln, c'est différent ?

Petit résumé des notations

J'ai également vu O(log₂ n). C'est quoi ce truc ?